In this blog, we will uncover the Vedic Geometry Origins in Ancient India, focusing on the Sulbha Sutras that detail the geometric principles used in Vedic rituals. This exploration will highlight how ancient Indian scholars laid the groundwork for geometry, influencing not just their civilization but the world at large.
Table of Contents
- Introduction
- The Three Fires
- The Origins of Geometry
- Who authored Sulbasutras
- How do we calculate sun’s position
- Units of Measure
- Types of Chitis or Fire Altars in Sulbha Sutras
- Types of Chitis
- Real Size of Chitis
- Geometric Transformations
- Pythagoras Theorem
- Example
- Other Examples
- Sindhu Saraswati Civilization
- Circle Construction
- Outro
- FAQ
Introduction
The study of geometry is not merely an academic pursuit; it is a window into the practical and philosophical foundations of ancient cultures. In the context of Vedic Geometry Origins in Ancient India, geometry was deeply intertwined with rituals and daily life. This blog will explore key concepts that not only define ancient Indian geometry but also highlight its relevance in today’s world.
The Three Fires
The concept of the three fires, known as Tretagni, is crucial in understanding Vedic geometry. Each fire represents a distinct geometrical shape and serves a unique purpose in Vedic rituals. The three fires are:
- Ahavaniya Agni: This fire is represented by a square altar and is primarily used for Vedic rituals.
- Graha Patya: Shaped as a circle, this altar is used for household purposes, such as cooking.
- Dakshin Agni: In the form of a semicircle, this altar symbolizes respect towards ancestors.
These three geometrical shapes—square, circle, and semicircle—form the foundation of Vedic geometry. Importantly, all three altars must maintain the same area, underscoring the mathematical sophistication of ancient Indian scholars.

The Origins of Geometry
The genesis of geometry in ancient Bharat is rooted in practical needs and ritualistic requirements. The Sulbha Sutras provide a codified understanding of geometry, detailing the construction of fire altars and their dimensions. This ancient text illustrates how geometry was applied in real-world scenarios, making it a practical discipline rather than just a theoretical one.
Moreover, the use of rope for geometric constructions allowed for flexibility and precision, showcasing the ingenuity of ancient mathematicians. This method was not just about creating shapes; it was a harmonious blend of art, science, and spirituality.

Who authored Sulbasutras
The Sulbha Sutras were authored by revered sages, known as rishis, who meticulously documented the principles of geometry. Some of the prominent authors include:
- Baudhayana: Often regarded as one of the oldest, his contributions date back over three thousand years.
- Apastamba: Another significant contributor, known for his systematic approach to geometry.
- Maitrayana and Katyaayana: Each brought their unique perspectives and methods to the study of geometry.
These texts are integral to the Yajurveda and serve as a testament to the rich mathematical heritage of ancient India.

How do we calculate sun’s position
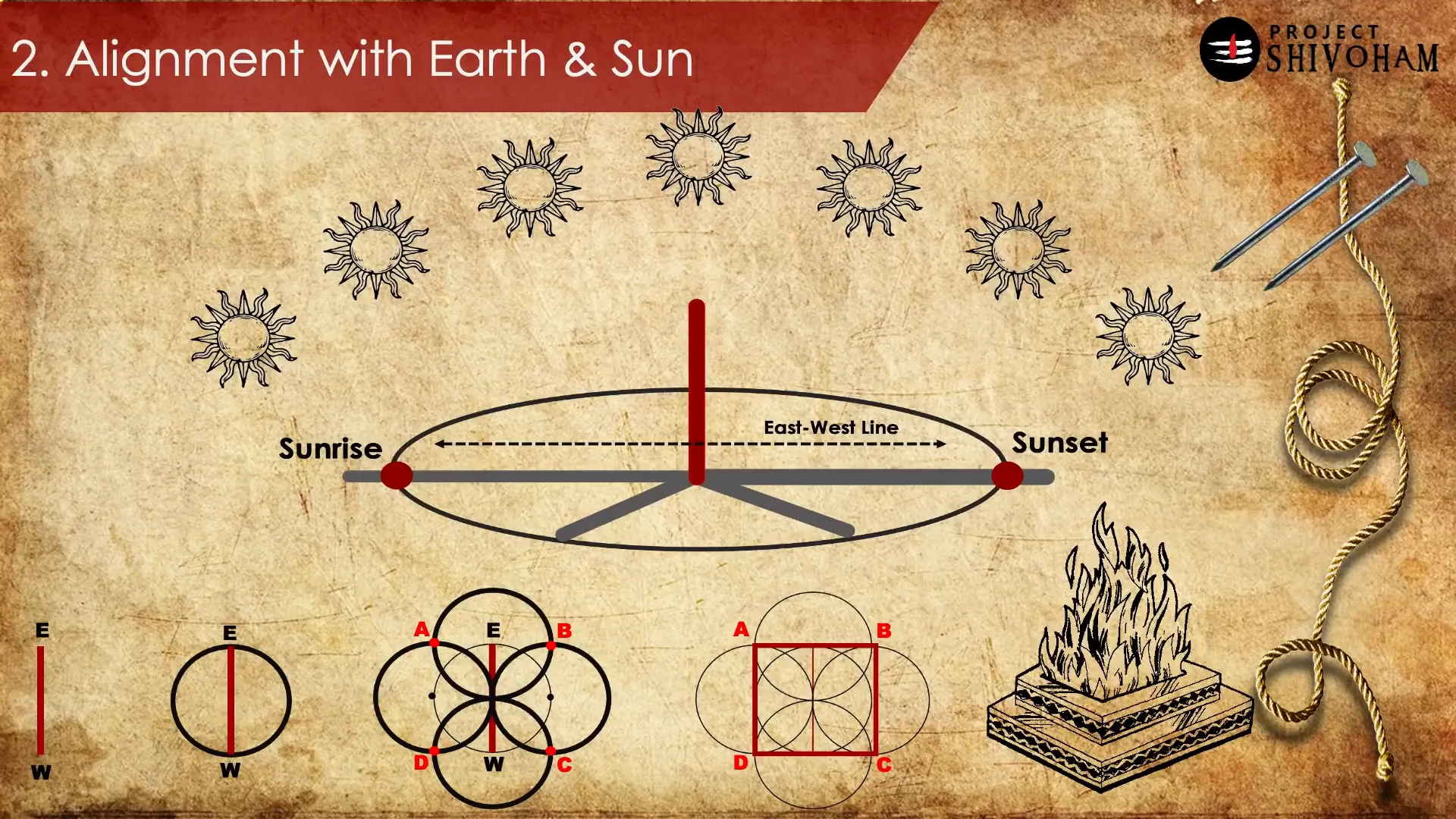
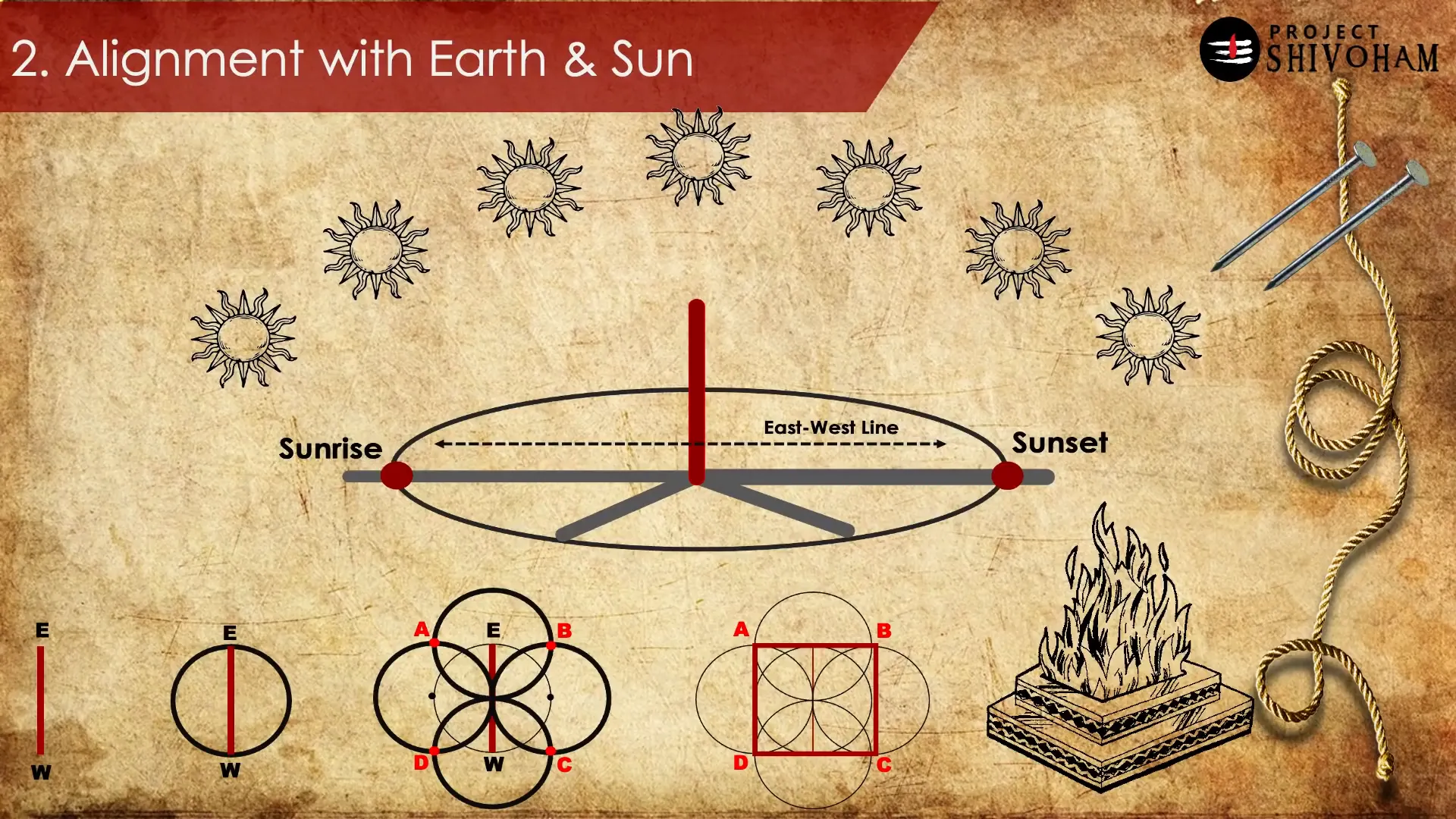
Understanding the position of the sun is essential for many Vedic rituals. The Sulbha Sutras provide a systematic approach to track the sun’s movement throughout the day. A simple yet effective method involves planting a vertical stick and drawing a circle around it with a thread.
As the sun rises and sets, the shadow of the stick will intersect the circle at two points. By connecting these points, one can establish the east-west line. This ability to calculate the sun’s position accurately is a testament to the advanced understanding of celestial mechanics by ancient Indian scholars.
Units of Measure
Geometry cannot exist without a system of measurement. The Sulbha Sutras introduce various units of measure essential for constructing fire altars and conducting rituals. One of the most notable units is the Angula, which is defined as the length of thirty-four sesame seeds stacked face to face.
This unit of measure was practical and relatable, allowing ancient builders to communicate dimensions effectively. For instance, one hundred and twenty Angulas was considered the height of an average human, referred to as one Purusha.

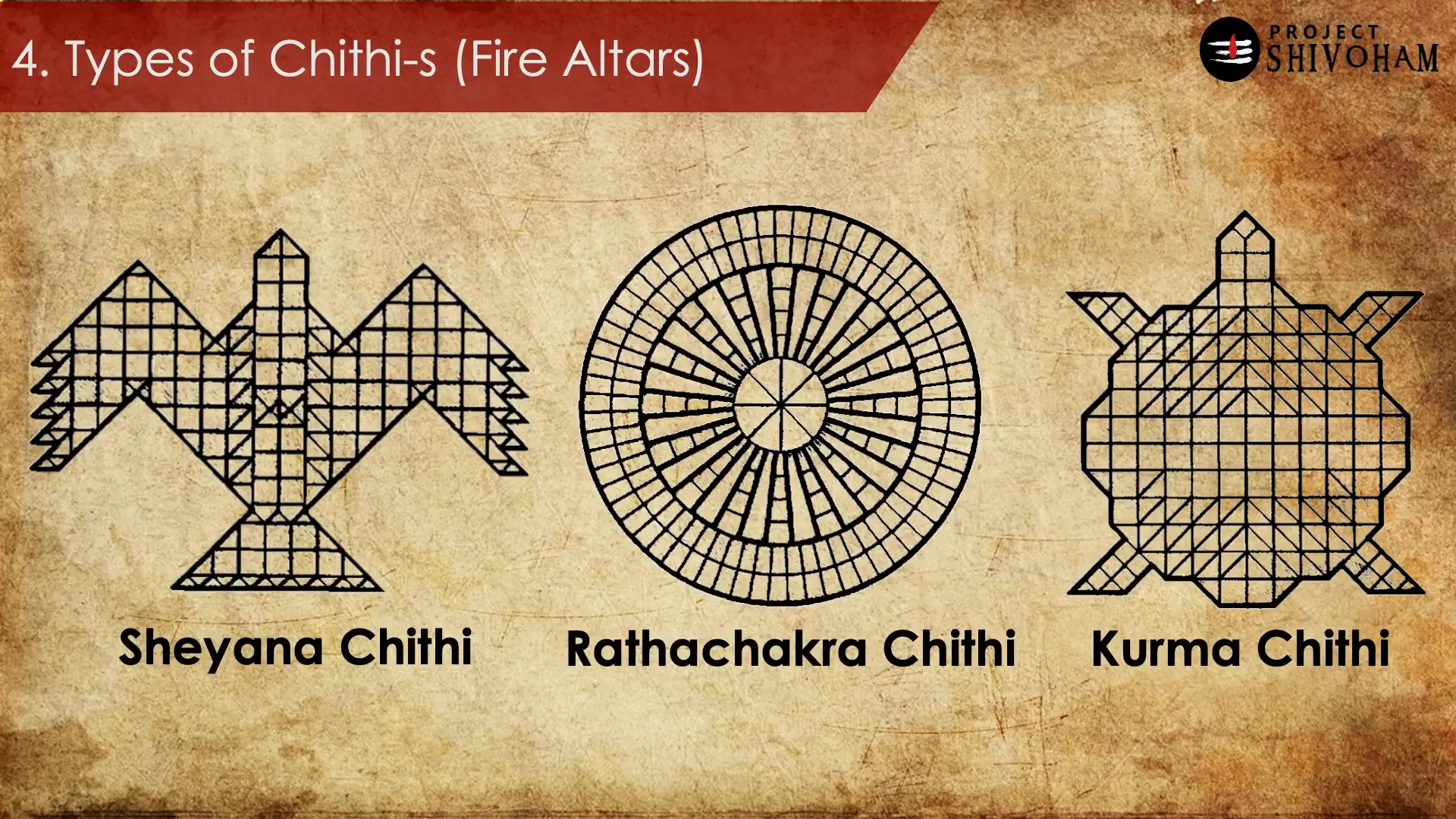
Types of Chitis or Fire Altars in Sulbha Sutras
The complexity of fire altars, known as chitis, is a significant aspect of the Sulbha Sutras. While initial altars like the Tretagni are relatively simple geometrical shapes, others are intricate arrangements of bricks that must be cut with precision.
Some notable types include:
- Shayana Chitti: Resembling the shape of a falcon, this altar requires a variety of geometric shapes for its construction.
- Radha Chakra Chitti: Another complex design that showcases the geometrical prowess of ancient builders.
Each altar’s design reflects not only mathematical principles but also cultural significance, emphasizing the intertwining of geometry with spirituality.
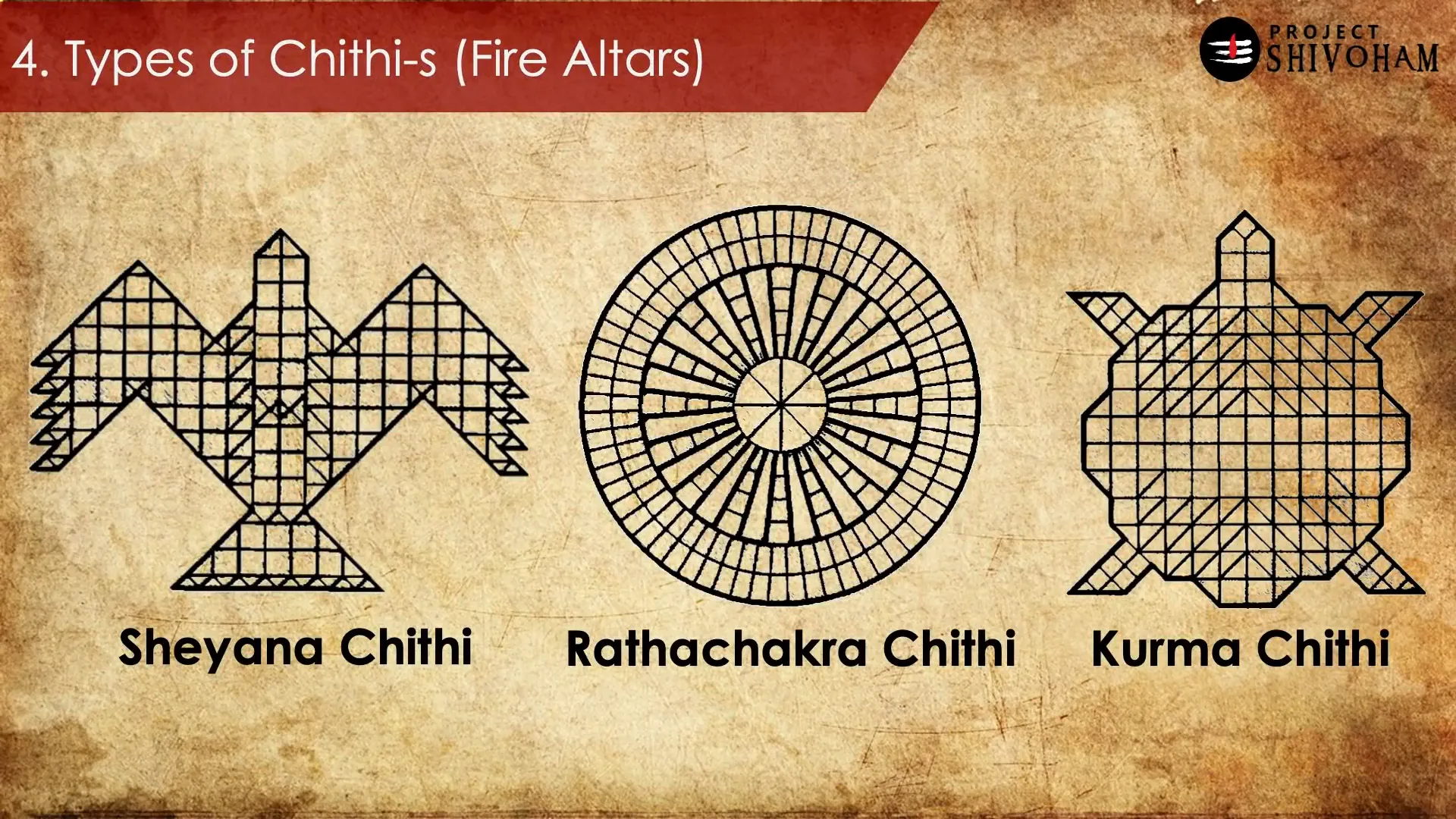
Types of Chitis
The Sulbha Sutras describe various types of chitis, or fire altars, each with unique geometrical designs and purposes. These designs reflect the sophistication of Vedic geometry and the spiritual significance behind each altar. Some notable types include:
- Shayana Chitti: This altar is shaped like a falcon and utilizes a combination of geometric forms for its construction.
- Radha Chakra Chitti: A complex altar that showcases intricate geometric arrangements, illustrating the advanced understanding of geometry.
- Kurma Chitti: Representing a tortoise, this altar involves precise geometric calculations and arrangements of bricks.
These chitis demonstrate how geometry was not merely a mathematical exercise but was deeply integrated into the spiritual practices of ancient India.
Real Size of Chitis
The real size of chitis varies based on the ritual and the specific requirements outlined in the Sulbha Sutras. For example, the Shayana Chitti, which resembles a falcon, is constructed with bricks that are meticulously shaped and sized to ensure structural integrity and alignment with Vedic principles.
Each brick used in the construction of these chitis must be uniform, adhering to the geometric principles laid out in the scriptures. The dimensions of these bricks are not arbitrary; they are calculated to achieve the desired area and volume for the altar.

Geometric Transformations
Geometric transformations play a crucial role in the construction of fire altars, allowing for the manipulation of shapes while maintaining the same area. The Sulbha Sutras detail methods for transforming one geometric figure into another, which is essential for the precise cutting of bricks needed for various altars.
For instance, one can start with a square and transform it into a rectangle of equal area or triple the area of the original square using specific geometric operations. This capability is vital for ensuring that the materials used align with the required dimensions for Vedic rituals.

Pythagoras Theorem
The Pythagorean theorem, known in Sanskrit as Bujakoti Karani Nyayam, is a foundational principle in Vedic geometry. It describes the relationship between the sides of a right triangle, providing a method for determining the length of the diagonal when the lengths of the other two sides are known.
This theorem is not just a theoretical concept; it was practically applied in ancient India for constructing right-angled shapes essential for the design of fire altars. The Sulbha Sutras outline the necessary calculations and geometric principles to utilize this theorem effectively.

Example
To illustrate the application of the Pythagorean theorem, consider an example from the Sulbha Sutras. Suppose we need to triple the area of a given square. Starting with a square of side length ‘a’, we can calculate the diagonal using the Pythagorean theorem.
According to the theorem, the diagonal (d) can be found using the formula: d = √(a² + a²) = a√2. By applying this diagonal as one side of a rectangle, we can then compute the dimensions required to achieve a square with three times the area of the original square.

Other Examples
Beyond the examples provided, the Sulbha Sutras contain numerous applications of geometric transformations. For instance, the process of converting a square into a circle while maintaining the same area is a challenge that has intrigued mathematicians for centuries.
The guidelines in the Sulbha Sutras offer a systematic approach to achieving this transformation, showcasing the ancient Indian understanding of geometry. These principles not only serve practical purposes in rituals but also highlight the mathematical innovation present in ancient Bharat.

Sindhu Saraswati Civilization
The Sindhu Saraswati Civilization, often referred to as the Indus Valley Civilization, is a cornerstone of ancient Indian history. Flourishing over five thousand years ago, this civilization showcased remarkable advancements in various fields, including geometry. One of the most impressive aspects of this civilization was its use of bricks.
Researchers have discovered that the bricks used in the Sindhu Saraswati civilization adhered to a specific dimension ratio of 4:2:1. This ratio is not arbitrary; it represents one of the most optimal dimensions for structural integrity. Such precise measurements suggest a deep understanding of geometry and its applications in construction.

Geometric Expertise in Construction
Another fascinating feature of the Sindhu Saraswati civilization is its adeptness in constructing right-angled structures using circles. The ancient builders understood that a vertical line intersecting a horizontal line at the center of a circle creates a perfect right angle. This principle is foundational in geometry and demonstrates the civilization’s sophisticated knowledge of geometric constructions.
This method of deriving right angles using circles resonates with the practices outlined in the Vedic rituals, where circles were also used for similar purposes. Such commonalities hint at a shared cultural and mathematical heritage, emphasizing the importance of geometry in both the Sindhu Saraswati civilization and ancient Vedic practices.

Circle Construction
Circle construction is a pivotal aspect of Vedic geometry, particularly in the context of creating fire altars and other sacred structures. The ancient scholars employed methods to accurately draw circles, which were essential for aligning structures with cardinal directions and celestial events.
One notable technique involved using a rope to define the radius of the circle. By anchoring one end of the rope at a central point and rotating the other end around it, a perfect circle could be constructed. This method not only ensured precision but also allowed for the flexible adjustment of the circle’s size according to specific ritual requirements.
The Role of Circles in Vedic Rituals
Circles held profound significance in Vedic rituals. They were often associated with the concept of completeness and wholeness, symbolizing the cyclical nature of life and the universe. The act of constructing a circle was not merely a geometric exercise; it was imbued with spiritual meaning and purpose.
In the construction of fire altars, circles were utilized to demarcate sacred spaces and ensure that rituals were performed in alignment with cosmic principles. This connection between geometry and spirituality illustrates how ancient Indian scholars viewed mathematics as an integral part of their cultural and religious practices.

Outro
The exploration of Vedic geometry origins in ancient India reveals a rich tapestry of knowledge that has stood the test of time. From the sophisticated designs of the Sindhu Saraswati civilization to the detailed instructions in the Sulbha Sutras, the mathematical prowess of ancient Indian scholars is evident.
As we reflect on these contributions, it becomes clear that geometry was not merely a tool for construction but a means of connecting with the divine. The principles laid out in the Sulbha Sutras and the practices of the Sindhu Saraswati civilization continue to inspire modern mathematicians and researchers alike.
For those keen on delving deeper into this fascinating subject, a wealth of resources awaits. The Sulbha Sutras, in particular, offer a treasure trove of insights into the mathematical innovations of ancient Bharat. Exploring these ancient texts can provide a greater appreciation for the foundational role that geometry played in shaping civilization.

FAQ
What are the Sulbha Sutras?
The Sulbha Sutras are ancient Indian texts that codify the principles of geometry and construction, particularly concerning Vedic rituals. They provide instructions on how to construct fire altars and other geometrical shapes essential for religious practices.
How did the Sindhu Saraswati civilization use geometry?
The Sindhu Saraswati civilization employed geometric principles in various aspects, notably in the construction of bricks with optimal dimensions for structural integrity. They also used circles to derive right angles, showcasing their advanced understanding of geometry.
What is the significance of circles in Vedic geometry?
Circles in Vedic geometry symbolize completeness and are crucial for aligning structures with cosmic principles during rituals. They represent the cyclical nature of life and are integral to the construction of fire altars.