The concept of negative numbers has a rich history that traces back to ancient civilizations, particularly in Bharat. This blog explores the negative numbers origin in ancient India, highlighting significant contributions from scholars like Brahmagupta and ancient texts that shaped our understanding of mathematics.
Table of Contents
- Intro
- Rules on ADDITION of Positives, Negatives & Zero
- The Bakhshali Manuscript
- Surya Siddhantam Orbital Velocity Calculations
- History of Negative Numbers in Bharat
- Conclusion
- FAQ
Intro
The exploration of negative numbers offers a fascinating glimpse into the evolution of mathematical thought. The negative numbers origin in ancient India showcases how early mathematicians grappled with concepts that would later become fundamental to modern mathematics. This journey begins with the understanding of numbers as not just mere symbols, but as representations of quantities that can be positive, negative, or even neutral.
Why Negative Numbers…?
Negative numbers are essential for various reasons. First, they allow for a more comprehensive understanding of the number line, where every point represents a unique quantity. They also facilitate calculations involving debts, losses, and temperature differences, making them indispensable in daily life.
In ancient times, many civilizations struggled to grasp the idea of numbers less than zero. The concept of debt or loss was often abstract and not formally defined. However, ancient Indian scholars, particularly Brahmagupta, made significant strides in recognizing the importance of negative numbers and integrating them into mathematical operations.
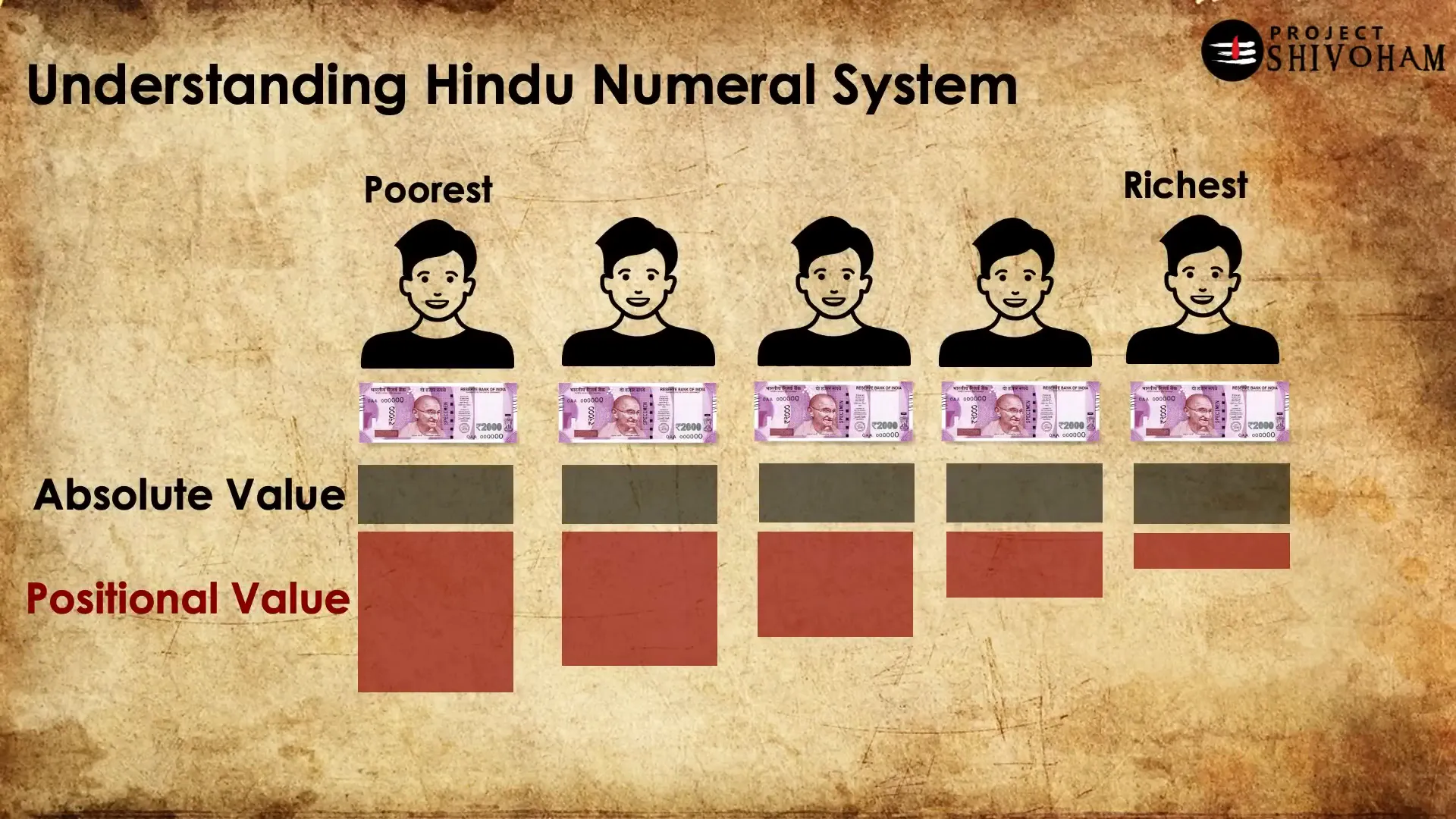
Understanding Hindu Numeral System
The Hindu numeral system, which is widely used today, is rooted in the positional value system. Each digit’s position within a number determines its value, allowing for a more efficient representation of large numbers. This system also includes the use of zero, which was revolutionary in its time.
In this context, the understanding of negative numbers becomes clearer. The system not only accommodates positive integers but also provides a framework for representing negative quantities. This duality is a hallmark of the Hindu numeral system, which distinguishes it from other ancient counting systems.
Decoding Brahmagupta…
Brahmagupta’s work, particularly in his treatise Brahmasputasiddhantam, is crucial for understanding the arithmetic of positive and negative numbers. He codified rules that describe how to add, subtract, multiply, and divide these numbers, setting the foundation for future generations of mathematicians.
In the eighteenth chapter of his work, Brahmagupta introduces three key terms: Dhanam (positive quantity), Sunyam (zero), and Runam (negative quantity). Each of these terms plays a significant role in the operations he describes, highlighting the interconnectedness of these concepts.

Definition of Negatives & Positives…
Brahmagupta’s definitions of positive and negative numbers challenge contemporary perceptions. He viewed positive numbers (Dhanam) and negative numbers (Runam) as transient states in relation to zero (Sunyam), which he considered the ultimate stable state. This perspective encourages a reevaluation of how we understand the relationship between these quantities.
In modern terms, we often think of negative numbers as being less than zero. However, Brahmagupta’s approach emphasizes that both positive and negative numbers represent movement relative to a point of reference, which can be zero or any other number. This understanding opens up new avenues for interpreting mathematical operations and their implications.

Rules on ADDITION of Positives, Negatives & Zero
Brahmagupta established foundational rules for the addition of positive and negative numbers, which are crucial for understanding arithmetic operations. His rules provide clarity on how to handle different combinations of numbers.
- Positive + Positive: The sum of two positive numbers is always positive. This reflects straightforward addition.
- Negative + Negative: The sum of two negative numbers is also negative. This signifies a deeper loss or debt.
- Positive + Negative: The result depends on the magnitudes of the numbers. If the positive number is greater, the result is positive; if the negative number is greater, the result is negative.
- Zero: Adding zero to any number leaves the number unchanged, reinforcing the concept of zero as a neutral element.

Rules on SUBTRACTION of Positives, Negatives & Zero
Subtraction introduces complexity due to its relation to negative outcomes. Brahmagupta’s rules for subtraction clarify these operations.
- Positive – Positive: When subtracting a smaller positive from a larger positive, the result is positive. Conversely, subtracting a larger positive from a smaller positive yields a negative result.
- Negative – Negative: Subtracting a negative from another negative can lead to a positive result, depending on the magnitudes involved.
- Zero: Subtracting zero from a positive or negative does not change the quantity, leaving it unchanged.

Rules on DIVISION of Positives, Negatives & Zero
Division, like subtraction, has its own set of rules that Brahmagupta meticulously outlined, ensuring clarity in operations involving zero and negative numbers.
- Positive ÷ Positive: The result is always positive.
- Negative ÷ Negative: The result is positive, as two negatives yield a positive outcome.
- Positive ÷ Negative: This results in a negative outcome, reflecting the inherent contradiction in dividing a positive by a negative.
- Zero ÷ Zero: Brahmagupta noted that this results in zero, although dividing any number by zero is typically considered undefined.

The Bakhshali Manuscript
The Bakhshali Manuscript is a historical text that predates Brahmagupta, dating back to around 200-250 CE. It is significant for its insights into early Indian mathematics, especially concerning negative numbers and subtraction.
Written in the Sharada script, the manuscript includes various arithmetic operations and demonstrates an understanding of negative quantities, albeit in a less formalized manner than Brahmagupta’s later codifications.

Arithmetic Operations in the Bakhshali Manuscript
Within the Bakhshali Manuscript, operations such as addition and subtraction are represented in a way that hints at the early use of negative numbers. For example, the manuscript illustrates equations where the results may naturally lead to negative outcomes.
Notably, the representation of numbers and operations suggests a sophisticated understanding of arithmetic that was ahead of its time. The manuscript’s treatment of negative numbers paved the way for later mathematicians, including Brahmagupta.

Surya Siddhantam Orbital Velocity Calculations
Another significant text is the Surya Siddhantam, an ancient astronomical treatise that also contributes to the understanding of negative numbers. This scripture provides a framework for calculating the orbital velocities of celestial bodies.
In the Surya Siddhantam, the terms Dhanam and Runam are used to describe increases and decreases in orbital velocity, respectively. This application of positive and negative concepts in a physical context illustrates an advanced understanding of mathematics in ancient India.

Understanding Dhanam and Runam
The definitions provided in the Surya Siddhantam reflect a broader mathematical philosophy that aligns with Brahmagupta’s later work. Dhanam represents an increase in velocity when a planet approaches a massive body, while Runam indicates a decrease when moving away.
This duality of terms captures the essence of positive and negative numbers as more than mere abstract concepts; they have real-world applications in the study of astronomy and physics.

History of Negative Numbers in Bharat
The history of negative numbers in Bharat is intertwined with the broader narrative of mathematical development within ancient Indian civilization. While Brahmagupta is often credited with formalizing rules concerning negative numbers, the origins of these concepts are far more complex and date back to earlier texts.
One notable text is the Bakhshali Manuscript, which hints at the use of negative quantities in arithmetic operations. This manuscript illustrates that Indian mathematicians were grappling with the concept of debts and losses well before Brahmagupta’s time.

As we delve deeper, we find that texts like the Surya Siddhantam also contributed significantly to the understanding of negative numbers. The Surya Siddhantam not only includes advanced calculations involving celestial bodies but also incorporates the sine function, which leads to handling negative quantities.

It’s essential to recognize that while Brahmagupta’s contributions are vital, he was building upon a foundation laid by earlier scholars. The evolution of mathematical thought in Bharat reflects a continuous dialogue among mathematicians who explored and expanded upon each other’s ideas.
Comparative Perspectives: Bharat and Other Civilizations
When examining the history of negative numbers, it’s crucial to consider the contributions from other ancient civilizations, particularly China. The mathematical operations involving negative numbers in ancient Chinese texts appear to predate those in Bharat, suggesting a parallel evolution of mathematical thought.
This comparative perspective highlights the rich tapestry of mathematical history, where different cultures contributed to the understanding of negative numbers independently. However, the depth of knowledge and the systematic approach taken by Indian scholars, particularly in the context of arithmetic operations, is noteworthy.

The Role of Cultural Perception
The perception of negative numbers has varied significantly across cultures. In Bharat and China, negative numbers were embraced as part of the mathematical framework, essential for understanding debts and losses. In contrast, European scholars historically viewed negative numbers with suspicion, often labeling them as “evil” or “satanic” until relatively recently.
This cultural bias against negative numbers in Europe is a stark contrast to the acceptance and integration seen in Bharat. It underscores the importance of recognizing the contributions of Asian civilizations in shaping mathematical concepts.

Conclusion
The historical journey of negative numbers in Bharat illustrates a rich mathematical legacy that has been overlooked in mainstream discussions. From the early explorations in the Bakhshali Manuscript to the systematic rules laid out by Brahmagupta, the contributions of Indian mathematicians have been pivotal in understanding negative quantities.
Moreover, the acceptance of negative numbers in Bharat stands in stark contrast to the historical perceptions in Europe, highlighting a cultural divide in the acceptance of mathematical concepts. As we continue to uncover the mathematical heritage of Bharat, it becomes increasingly clear that these contributions are not only significant but foundational to the development of mathematics as we know it today.
FAQ
What is the significance of negative numbers in mathematics?
Negative numbers are essential for representing values less than zero, facilitating calculations involving debts, losses, and differences in temperature. They expand the number line beyond positive values, allowing for a more comprehensive understanding of mathematical relationships.
Who was Brahmagupta, and what was his contribution to negative numbers?
Brahmagupta was a 7th-century Indian mathematician who formalized rules for arithmetic operations involving negative numbers in his work, Brahmasputasiddhantam. He introduced key terms for positive, zero, and negative quantities, laying the groundwork for future mathematical operations.
How did ancient Indian scholars view negative numbers?
Ancient Indian scholars viewed negative numbers as an integral part of mathematics. They recognized their utility in representing debts and losses, and their acceptance in arithmetic operations was notably more progressive compared to contemporary views in other civilizations, such as Europe.
Where can I learn more about the history of mathematics in Bharat?
To explore the history of mathematics in Bharat, consider reading ancient texts like the Bakhshali Manuscript, Surya Siddhantam, and Brahmasputasiddhantam. These texts provide insight into the mathematical principles and operations that shaped early Indian mathematics.