Unveiling Cryptography in Ancient India: More Than Just Secrets

Cryptography, often associated with the art of secrecy, has a fascinating history in ancient India where it served a unique purpose: enhancing the readability and memorization of knowledge. This blog explores the innovative techniques and systems utilized in ancient Indian scriptures, shedding light on a lesser-known aspect of this rich heritage.

Table of Contents

• Intro
• What’s Cryptography?
• The Origin of a Different Thought…
• Example of Katapayadi Notation
• Cryptography in Ancient India with Akshara Sankhya
• FAQ

Intro

Cryptography, a term often associated with secrets and hidden messages, has a rich and varied history. In ancient India, it was employed not merely to conceal information but to enhance the understanding and memorization of knowledge. This blog delves into the innovative methods employed in ancient Indian scriptures and education, revealing how cryptography played a pivotal role in the transmission of knowledge. By examining the techniques of articulation, we can appreciate the depth and sophistication of this ancient system.

What’s Cryptography?

At its core, cryptography is the art of encoding and decoding information. The term itself derives from the Greek word “kryptos,” meaning hidden. While modern interpretations often focus on secrecy, ancient Indian cryptography served a different purpose: making complex information more accessible and memorable.

In ancient India, cryptography was about clarity and understanding. Instead of merely hiding truths, it was about creating a framework that allowed knowledge to be easily transmitted and retained. This unique approach highlights the duality of cryptography as both a protective and an enlightening tool.

Techniques of Articulation in Ancient India for Verbal Transmission of Knowledge

The ancient Indian education system was rooted in oral tradition, emphasizing the direct transmission of knowledge from guru to shishya (student). This method ensured that knowledge remained fluid and accessible. To enhance this process, several techniques were employed:

• Rhythmic Techniques: The use of rhythm and meter, such as chanda shastra, made recitation engaging and easier to memorize.
• Dialectical Approaches: Storytelling and question-answer formats helped contextualize knowledge, making it relatable and easier to recall.
• Aphoristic Expressions: Condensing complex ideas into succinct sutras allowed for quick memorization and application.

These techniques were not just embellishments but essential tools for effective learning. They transformed the learning process into an art form, where knowledge was not only preserved but also celebrated.

Sushruta Samhita

The Sushruta Samhita is a foundational text in ancient Indian medicine and surgery, attributed to the sage Sushruta. It showcases the application of cryptography in articulating complex medical knowledge. The text is primarily written in Sanskrit, which was the scholarly language of the time.

In the Sushruta Samhita, medical concepts are often conveyed through aphoristic verses, which allowed practitioners to memorize intricate details about anatomy, surgical procedures, and medicinal plants. This method of encoding information ensured that essential medical knowledge was easily transmitted across generations.

Moreover, the use of cryptic expressions in the text facilitated a deeper understanding of the subject matter. For instance, specific terms used in Sushruta’s work denote various surgical instruments and techniques, which were not only practical but also poetic, reflecting the rich tradition of Sanskrit literature.

As a result, the Sushruta Samhita stands as a testament to the advanced medical knowledge of ancient India, illustrating how cryptography was employed not just for secrecy but to enhance the readability and applicability of vital information.

The Origin of a Different Thought…

The Akshara Sankhya system marks a pivotal moment in the evolution of numerical representation in ancient India. This system emerged from the need to articulate complex mathematical concepts using a language that could be memorized and recited easily. The underlying philosophy was to make knowledge accessible and applicable in daily life, ensuring that essential information was not only preserved but also actively utilized.

This approach to numbers was not merely functional; it was deeply rooted in the cultural and educational traditions of India. The emphasis on oral transmission necessitated a system that could encapsulate vast amounts of information in a concise form, allowing for easy recall. Thus, the Akshara Sankhya system was born, blending linguistic elements with numerical values to create a unique form of cryptography that served a different purpose than the modern understanding of the term.

Akshara Sankhya System of Aryabhatta

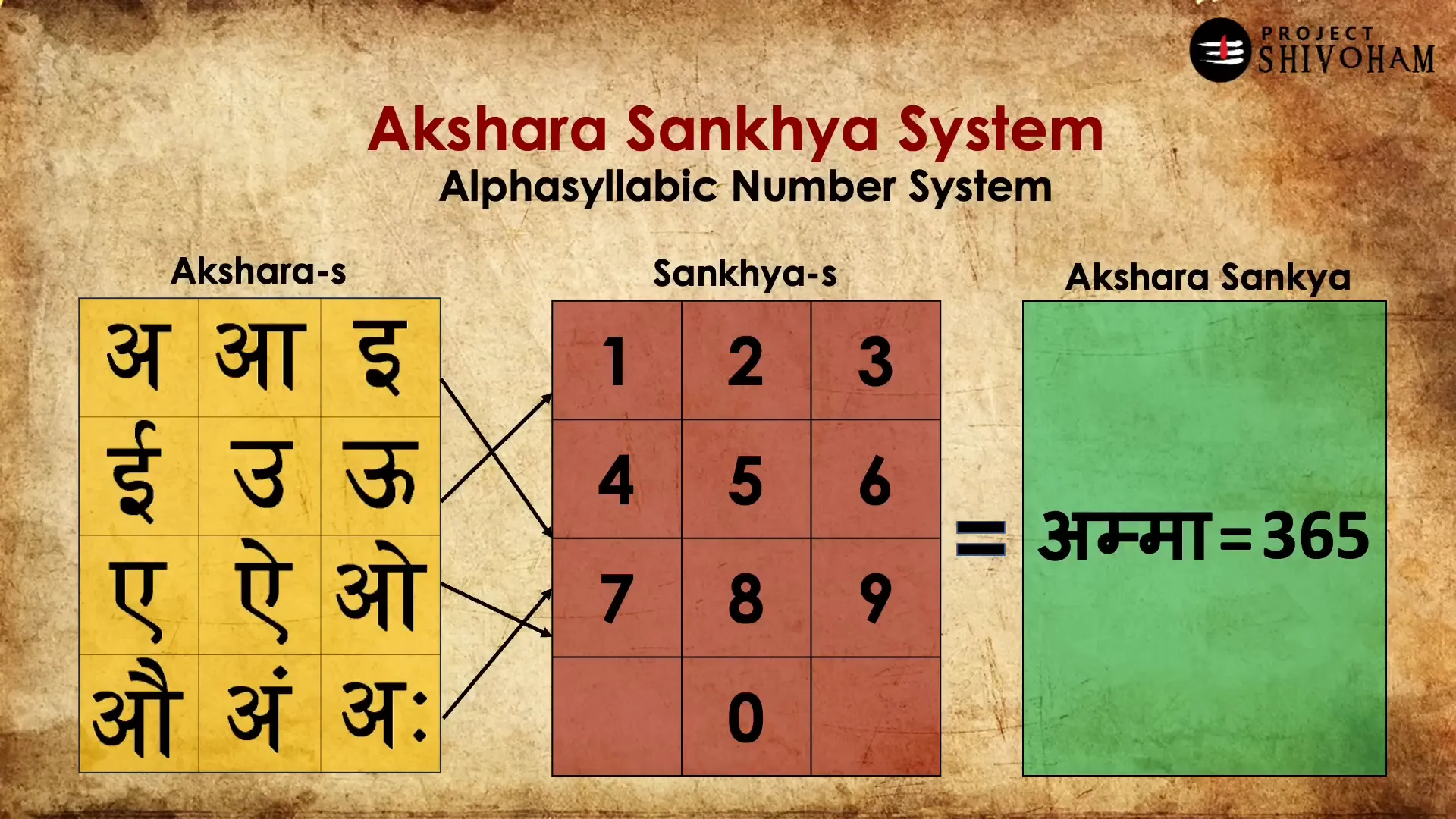
Aryabhatta, one of the most renowned mathematicians and astronomers of ancient India, significantly contributed to the Akshara Sankhya system. His innovative thinking allowed for the assignment of numerical values to the letters of the Sanskrit alphabet, creating a system where words could represent numbers. This made it easier to encode and transmit mathematical concepts in a poetic and rhythmic manner.

The beauty of the Akshara Sankhya system lies in its ability to convey complex numerical information through simple phonetic expressions. Each letter, or akshara, was assigned a specific numerical value, and by combining these letters, one could form words that represented large numbers. This system not only facilitated memorization but also kept the oral tradition alive, as students could easily recite long strings of numbers embedded within verses.

The Aryabhattan Akshara Sankya System

The Aryabhattan Akshara Sankhya system is a remarkable example of how language and mathematics can intertwine. Aryabhatta categorized vowels and consonants and assigned them powers of ten and numerical values respectively. For instance, the vowels represented powers of ten while consonants represented numerical values in a systematic way. This duality allowed for an expansive range of numbers to be expressed succinctly in Sanskrit.

In Aryabhatta’s framework, the vowels were essential in establishing the positional value of the consonants. This meant that a consonant alone could not convey a number without being accompanied by a vowel, thus creating a language that was inherently linked to its phonetic structure. The result was a sophisticated system that could express even the largest of numbers in a format that was not only practical but also lyrical.

Akshara Sankhya Notation for Sine Wave

The application of the Akshara Sankhya system extended beyond mere numerical representation; it played a crucial role in the development of trigonometry. Aryabhatta’s notation for the sine wave is a testament to this. He introduced the sine function in a way that was not only innovative but also deeply integrated into the existing linguistic and mathematical traditions of his time.

In his seminal work, Aryabhattiya, he articulated the sine function using a series of cryptic words that represented numerical values. This allowed for the sine wave to be expressed in a form that was both comprehensible and memorably recitable. The words he chose were not arbitrary; they were carefully selected to maintain the rhythmic and poetic nature of Sanskrit, thereby enhancing their memorability.

This cryptic yet functional approach to mathematics exemplifies how ancient scholars were able to bridge the gap between language and numerical representation, creating a system that was not designed to obscure knowledge but rather to illuminate it. The Akshara Sankhya system, therefore, stands as a remarkable achievement in the history of mathematics, showcasing the ingenuity of ancient Indian scholars.

Example of Katapayadi Notation

The Katapayadi system, developed in Kerala, is an innovative approach to numerical representation using the sounds of Sanskrit letters. This system assigns numerical values to letters, allowing for the encoding of numbers within words. For instance, the consonants and vowels are assigned specific values that correspond to a number. The brilliance of this system lies in its ability to make large numbers memorable and recitable.

To illustrate this, consider the word “Kalam,” which can represent the number 1000. Here, the consonant ‘K’ corresponds to a certain value, while the vowel ‘a’ adds a positional element. By combining these letters into words, scholars could encode significant numerical values seamlessly into their texts.

Using the Katapayadi system, complex information can be compressed into a single word or phrase. This serves not only as a mnemonic device but also as a way to convey deeper meanings within the context of the text. For instance, a poet might write a verse where the encoded values reflect the themes of longevity, prosperity, or knowledge, enriching the textual experience for the reader.

Cryptography in Ancient India with Akshara Sankhya

The Akshara Sankhya system, pioneered by Aryabhatta, represents a significant advancement in the field of cryptographic techniques in ancient India. By assigning numerical values to the letters of the Sanskrit alphabet, this system allowed for the encoding of complex mathematical concepts into easily memorized verses.

For example, Aryabhatta’s treatment of the sine function is a perfect illustration of this. He created a mnemonic verse that encoded the sine values into sounds that could be easily recited. Each syllable corresponded to a specific numerical value, allowing students to grasp intricate mathematical principles without the need for written numbers.

This approach not only facilitated easier learning but also preserved complex mathematical knowledge in a format that could be orally transmitted across generations. The Akshara Sankhya system exemplifies how ancient Indian scholars used cryptography not to obscure knowledge but to enhance its accessibility and memorability.

Moreover, these systems were deeply intertwined with the cultural and philosophical contexts of their time. They were designed not merely for practical use but also to reflect the beauty and rhythm of Sanskrit, making learning a more engaging and artistic endeavor.

FAQ

What is the Katapayadi system?

The Katapayadi system is a numerical representation technique that assigns values to letters in the Sanskrit alphabet, allowing for the encoding of numbers within words. It was developed in Kerala and is used to simplify the memorization of large numbers.

How does the Akshara Sankhya system work?

The Akshara Sankhya system assigns numerical values to vowels and consonants in Sanskrit. Vowels represent powers of ten, while consonants denote specific numbers. This allows for the formation of words that represent large numerical values, making them easier to memorize and recite.

What was the purpose of cryptography in ancient India?

In ancient India, cryptography was not primarily used for secrecy but rather to enhance readability and memorization of knowledge. Techniques like the Akshara Sankhya system allowed scholars to encode complex information in a way that was easy to recall and transmit orally.

How did Aryabhatta contribute to cryptography?

Aryabhatta contributed to cryptography through the development of the Akshara Sankhya system, which allowed for the encoding of mathematical concepts into memorable verses. His work in creating mnemonic devices for mathematical functions exemplifies the innovative use of language in ancient Indian education.

Why is this knowledge not widely taught today?

The achievements of ancient Indian scholars in fields like mathematics and cryptography are often overlooked in modern education. This may be due to a lack of awareness or appreciation for these contributions, highlighting the need for a broader understanding of historical knowledge systems.

Courtesy: Aravind Markandeya @ Project Shivoham