In this blog, we explore the rich mathematical heritage of ancient India, focusing on the algorithms that laid the groundwork for supercomputing. Discover the intricate relationship between language, rhythm, and advanced mathematics as we delve into the teachings of Maharshi Pingala Acharya.
Table of Contents
- Introduction
- Outline
- Background Context
- Chanda Sastram
- Algorithms on Super Computing
- Prasthara
- Binary Number System
- Nestum
- Udustam
- Meru Prasthara
- Maurya Prasthara History
- Key Takeaways
- Balanced Approach
- Conclusion
- FAQ
Introduction
The exploration of ancient Indian algorithms reveals a fascinating intersection of language, rhythm, and advanced mathematics. This blog continues the journey into the algorithms that have influenced supercomputing, shedding light on the contributions of ancient scholars and the sophisticated mathematical frameworks they employed.
Outline
- Introduction
- Background Context
- Chanda Sastram
- Algorithms on Super Computing
Background Context
The roots of advanced mathematics in Bharat can be traced back thousands of years. Understanding the context in which these algorithms were developed is essential. The ancient Indian education system, particularly the Vedic education system, was structured to facilitate the memorization and recitation of vast amounts of knowledge.

Chandra Shastra, a Vedanga, played a pivotal role in this system. It provided the rhythmic structure needed to memorize complex texts, ensuring that knowledge could be passed down through generations without the need for written documentation.
As we delve deeper into the algorithms, it becomes clear that the mathematical principles underpinning these ancient texts were not merely practical but also deeply artistic, merging the realms of language and mathematics.
Chanda Sastram
Chanda Sastram is the study of the rhythmic patterns within Sanskrit poetry. It provides a framework for constructing verses that are both harmonious and memorable. The principles of Chanda Sastram are not just about aesthetics; they involve intricate mathematical calculations that determine how syllables can be combined to fit into predefined rhythmic templates.

The beauty of Sanskrit lies in its structure. Each syllable has a specific weight—short syllables (laghoo) and long syllables (guru)—that must be balanced to create rhythmically sound verses. This balance is achieved through a series of algorithms that govern how words are constructed and arranged.
Algorithms on Super Computing
The algorithms developed by Maharshi Pingala Acharya form the backbone of Chanda Sastram and contribute significantly to the field of supercomputing. They enable the calculation of permutations and combinations of syllables, allowing for the efficient construction of words that adhere to rhythmic constraints.
Prasthara
Prasthara serves as a foundational algorithm in Chanda Shastram. This algorithm systematically generates all possible combinations of short (laghoo) and long (guru) syllables for a given word length. Understanding Prasthara is crucial for anyone looking to appreciate the depth of ancient Indian mathematical thought.
The essence of Prasthara lies in its ability to exhaustively enumerate syllable combinations. For instance, when constructing a four-letter word, Prasthara outlines all possible arrangements of laghoo and guru. This exhaustive list is essential because it allows the substitution of actual letters to create meaningful words that fit specific rhythmic templates.


One of the primary algorithms, Prasthara, provides a systematic approach to generating all possible combinations of syllables for a given word length. This method not only simplifies the construction of words but also reveals the underlying mathematical principles that govern these combinations.
Another crucial algorithm, Nashtam, allows researchers to identify the specific syllable sequence at any given position within the total possibilities. This is particularly useful for analyzing the structure of complex verses and understanding how different syllable combinations contribute to the overall rhythm.

Udishtam, the converse of Nashtam, calculates the position of a specific sequence within the larger set of combinations. This reciprocal relationship between the two algorithms highlights the intricate mathematical relationships present in Chanda Sastram.

The Sankhya algorithm is designed to calculate the total number of possible combinations for an n-letter word. This fundamental principle underscores the efficiency of the algorithms developed by Pingala Acharya, showcasing his advanced understanding of combinatorial mathematics.

Lastly, the Lagakriya algorithm introduces the concept of Meruprasthara, which is often mistakenly referred to as Pascal’s triangle. This triangular arrangement of numbers serves as a powerful computational tool, facilitating quick calculations of combinations and reinforcing the idea that ancient Indian mathematicians were light-years ahead in their understanding of mathematical concepts.

These algorithms collectively illustrate the sophisticated mathematical landscape of ancient India. They reveal how the interplay between language and mathematics was not only a means of artistic expression but also a precursor to modern computational methods.
Prasthara
Prasthara serves as a foundational algorithm in Chanda Shastram. This algorithm systematically generates all possible combinations of short (laghoo) and long (guru) syllables for a given word length. Understanding Prasthara is crucial for anyone looking to appreciate the depth of ancient Indian mathematical thought.
The essence of Prasthara lies in its ability to exhaustively enumerate syllable combinations. For instance, when constructing a four-letter word, Prasthara outlines all possible arrangements of laghoo and guru. This exhaustive list is essential because it allows the substitution of actual letters to create meaningful words that fit specific rhythmic templates.

At its core, the process follows a three-step methodology: identifying the syllables, mixing them, and repeating the mixing process recursively. This structured approach not only simplifies the task of word construction but also reveals underlying mathematical principles.

Binary Number System
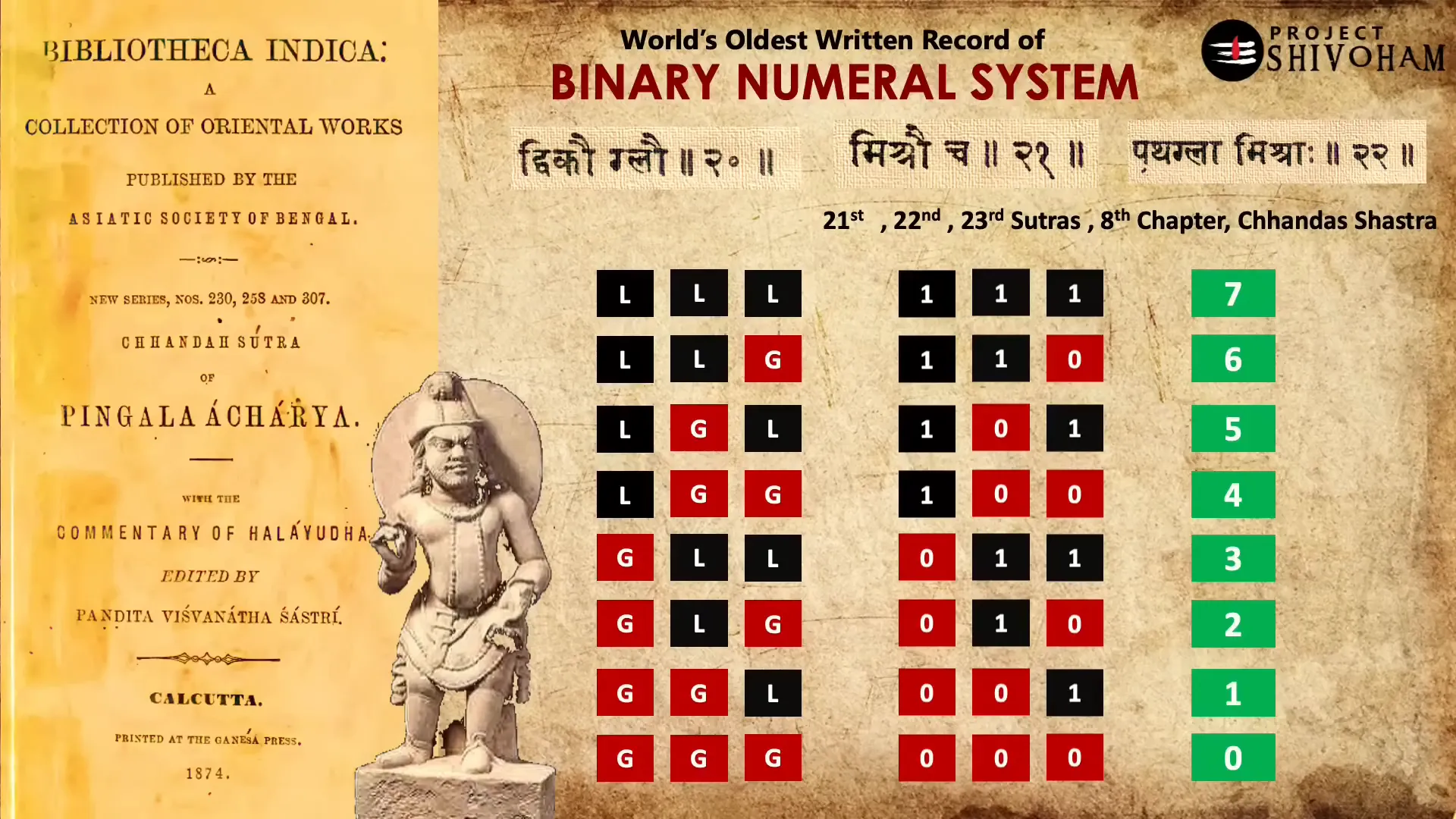
The connection between Prasthara and the binary number system is profound. The algorithm’s step-by-step mixing process mirrors the binary representation of numbers, where each syllable can be viewed as a binary digit. This relationship illustrates the ancient origins of concepts that are foundational in modern computing.

Specifically, the formula \(2^n\) emerges from this algorithm, where \(n\) represents the number of syllables. This insight not only showcases the sophistication of ancient Indian mathematics but also highlights how these early concepts laid the groundwork for contemporary computational theories.
Nestum
Nestum is another pivotal algorithm that works in conjunction with Prasthara. This algorithm allows one to determine the exact syllable sequence at a specific position within the total combinations generated. For example, in a four-letter word scenario with sixteen possible combinations, Nestum can pinpoint the seventh position’s syllable sequence.

The practical utility of Nestum is evident in its application to Sanskrit poetry, where precise syllable placement is vital for maintaining rhythm and meaning. This algorithm empowers scholars and poets alike to analyze and construct verses with accuracy.
Udustam
In contrast to Nestum, Udustam serves as the converse algorithm. It focuses on determining the position of a specific syllable sequence within the larger set of combinations. This reciprocal relationship between Nestum and Udustam exemplifies the intricate mathematical relationships embedded within Chanda Shastram.

By utilizing Udustam, one can efficiently navigate through the vast array of syllable combinations, establishing a clear framework for understanding how specific sequences fit into the overall structure of a word. This capability is invaluable for poets and mathematicians alike, enriching both the linguistic and numerical landscapes of ancient Indian scholarship.
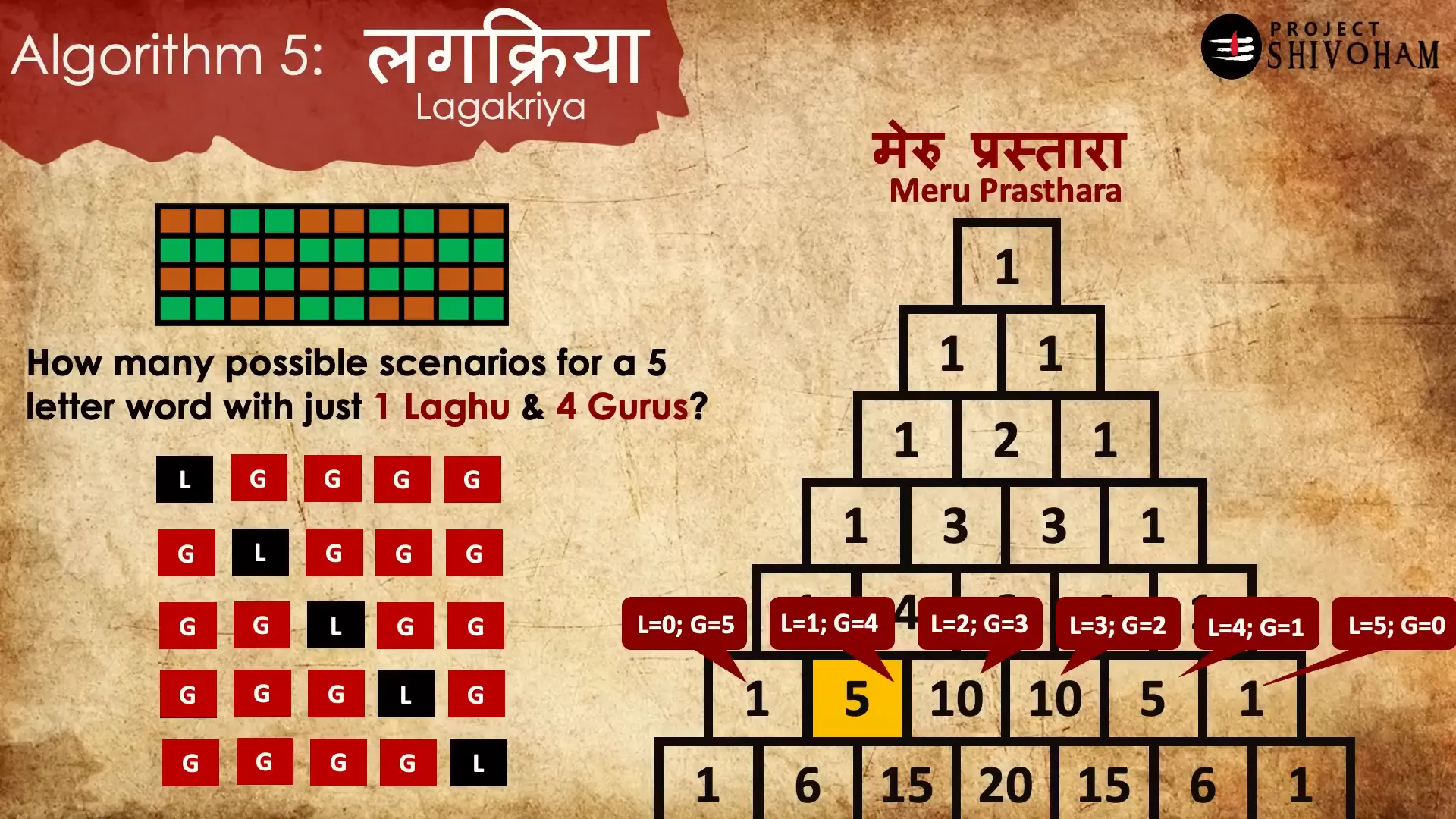
Meru Prasthara
Meru Prasthara, often misidentified as Pascal’s triangle, stands as one of the most sophisticated algorithms developed by Maharshi Pingala Acharya. This triangular arrangement of numbers provides a powerful computational tool for quickly determining the number of combinations possible for specific syllable arrangements.

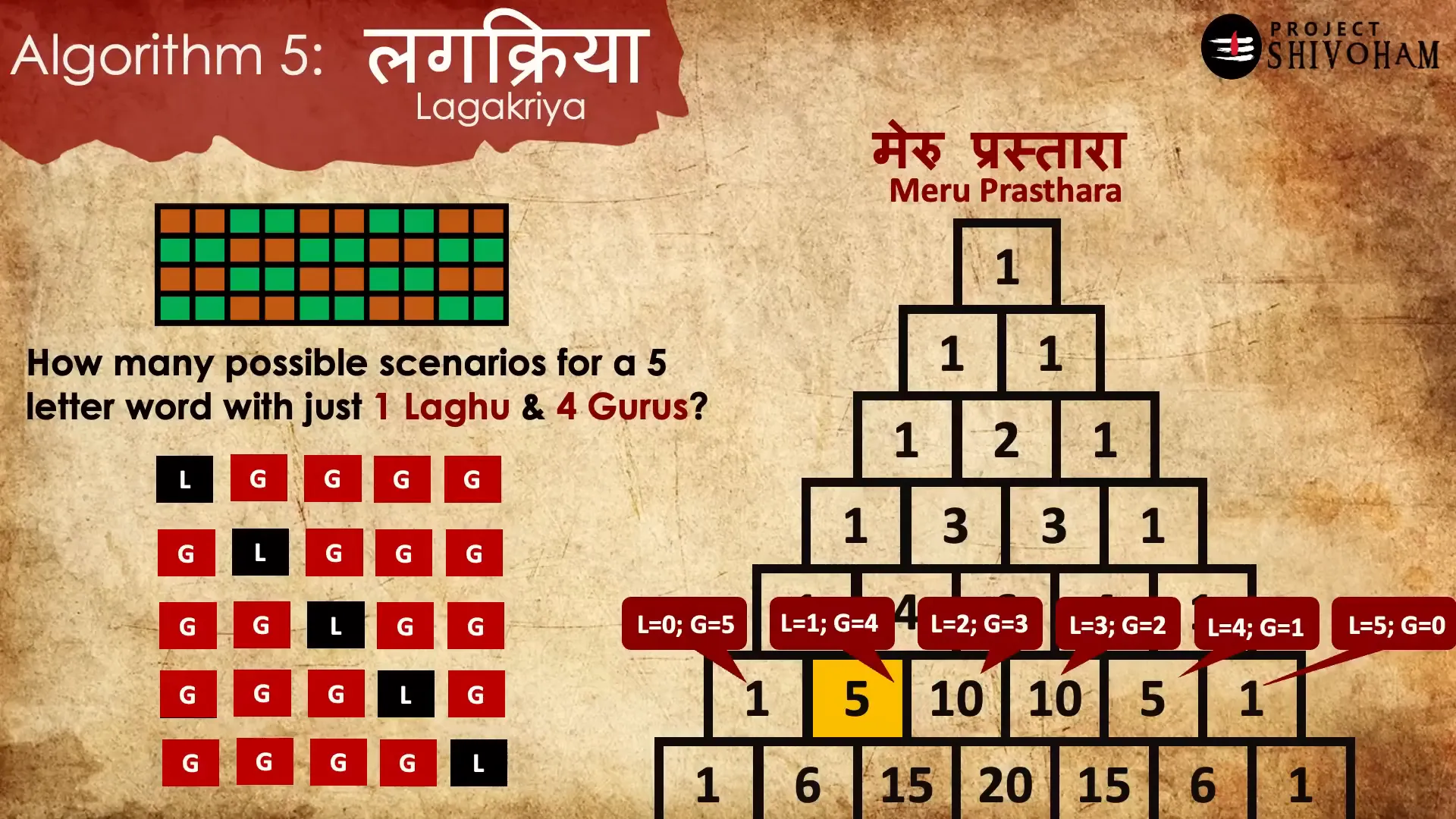
In the context of rhythmic templates, Meru Prasthara allows for rapid calculations regarding syllable combinations. For instance, if tasked with constructing a five-letter word with one laghu and four gurus, one can simply refer to the appropriate row of the triangle to derive the answer.
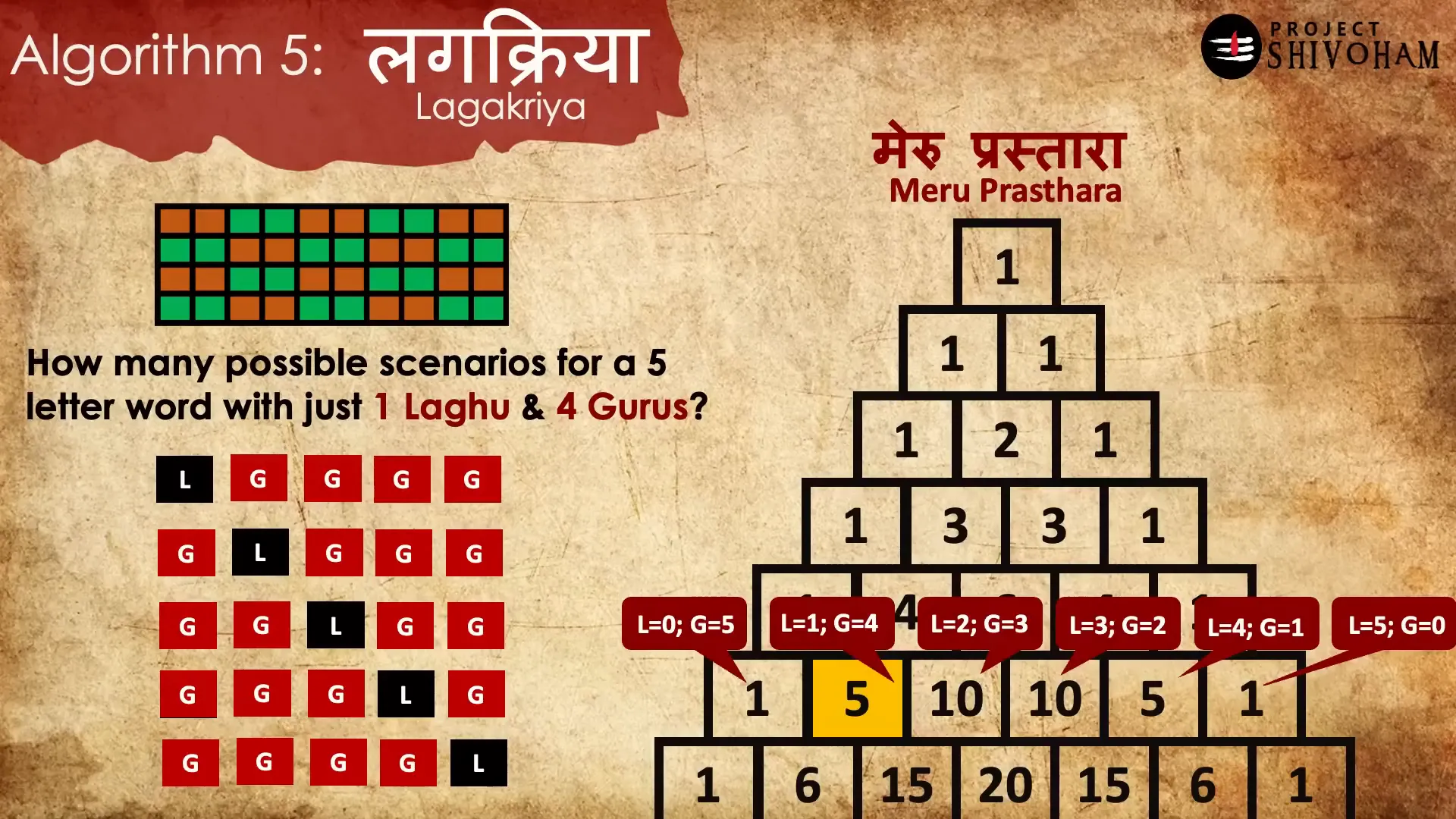
This algorithm not only simplifies complex calculations but also exemplifies the advanced mathematical thinking that characterized ancient Indian scholars. The efficiency and elegance of Meru Prasthara highlight the depth of knowledge within Chanda Shastram, showcasing how art and science intertwine seamlessly in the realm of Sanskrit poetry and mathematical theory.
Maurya Prasthara History
Maurya Prasthara is a significant mathematical concept originating from ancient India, particularly associated with the algorithms of Maharshi Pingala Acharya. This algorithm served as a foundational framework for constructing and analyzing syllable combinations within the context of Sanskrit poetry.
Historically, the Maurya Prasthara algorithm has been recognized for its systematic approach to generating combinations of syllables based on their lengths. This algorithm is not merely a tool for word construction; it symbolizes the advanced mathematical thinking present in ancient Indian scholarship.
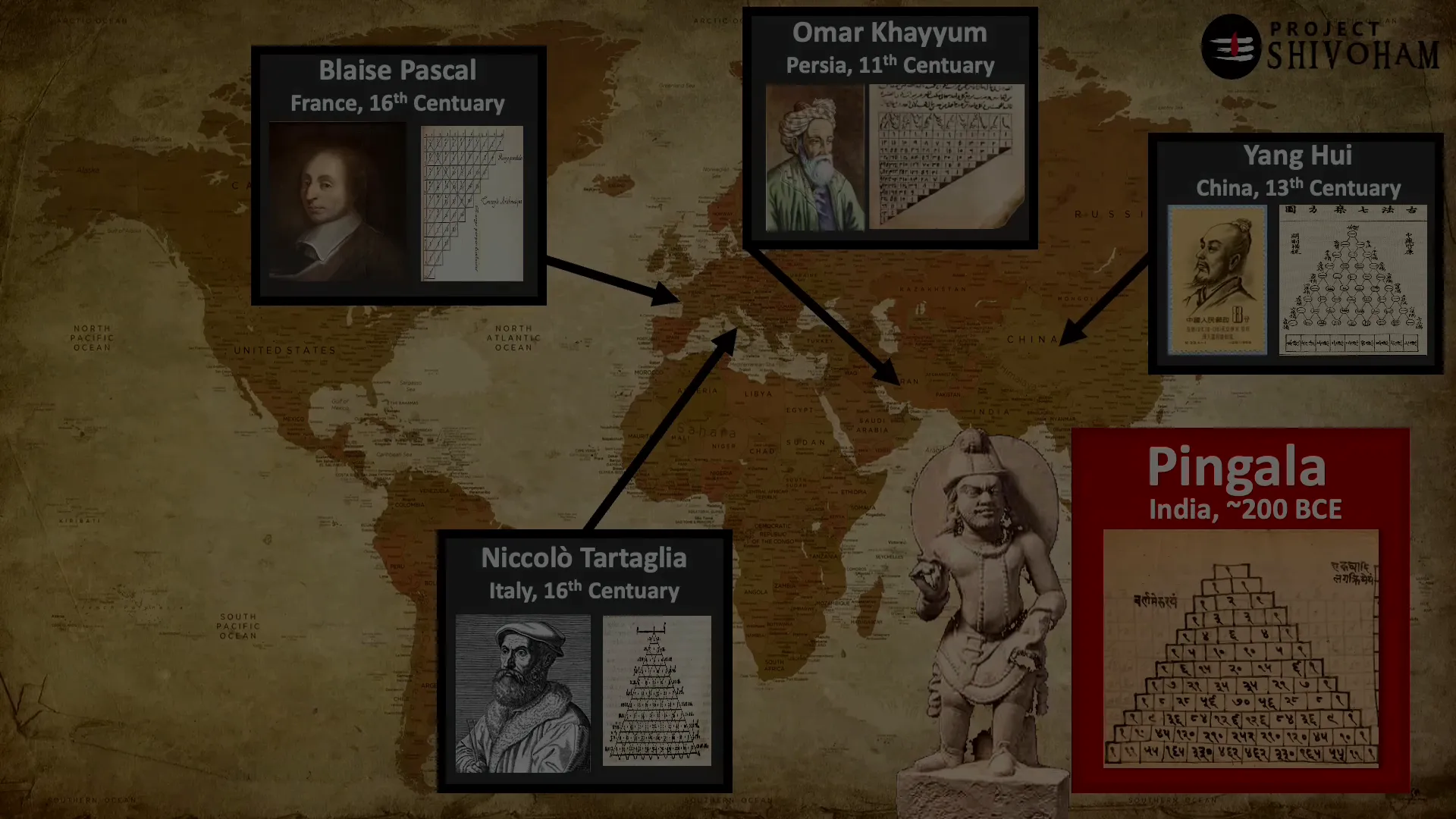
Dating back to around 200 BCE, the Maurya Prasthara has influenced various mathematical concepts, including what we now recognize as Pascal’s Triangle. The historical significance of this algorithm lies in its contributions to both mathematics and linguistics, showcasing the interconnectedness of these fields in ancient Indian culture.
How MeruPrasthara became Pascal’s triangle

Key Takeaways
Understanding the algorithms of Chandra Shastra, including Maurya Prasthara, reveals several key insights into ancient Indian mathematics.
- Art and Science Interconnected: The algorithms blur the lines between art and science. Chandra Shastra exemplifies how mathematical principles can underpin artistic expression, particularly in poetry.
- Historical Context: The evolution of these algorithms illustrates the rich mathematical heritage of Bharat. It challenges modern perceptions of ancient civilizations’ capabilities and highlights the depth of their knowledge.
- Linguistic Sophistication: The grammar of Sanskrit, as revealed through these algorithms, underscores its complexity. The structure of the language itself is a testament to the advanced thinking of ancient scholars.

Balanced Approach
In discussing the algorithms of ancient India, it is essential to maintain a balanced perspective. There are often polarized views on the achievements of ancient Indian mathematicians. Some may exaggerate their capabilities, while others may dismiss them entirely.
A balanced approach encourages critical analysis rather than blind acceptance or rejection. It fosters an understanding of the context in which these algorithms were developed and their relevance to both historical and contemporary mathematics.

Conclusion
The algorithms of Chandra Shastra, particularly Maurya Prasthara, represent a remarkable intersection of language, mathematics, and art. They provide insight into the sophistication of ancient Indian thought and its lasting impact on modern mathematical concepts.
As we explore these ancient algorithms, we uncover the depth of knowledge that has shaped not only Indian culture but also the broader landscape of mathematics. It is crucial to continue researching and appreciating these contributions as we move forward in understanding our mathematical heritage.

FAQ
What is the Maurya Prasthara algorithm?
Maurya Prasthara is an algorithm developed by Maharshi Pingala Acharya that systematically generates combinations of syllables in Sanskrit poetry, focusing on their lengths.
How does Maurya Prasthara relate to modern mathematics?
This algorithm is considered a precursor to several modern mathematical concepts, including Pascal’s Triangle, demonstrating the advanced mathematical thinking of ancient Indian scholars.
What role does Chanda Shastra play in Indian mathematics?
Chanda Shastra is a crucial aspect of Vedic studies, focusing on the construction of rhythmic patterns in poetry, which involves complex mathematical calculations for syllable combinations.
Why is it important to study ancient Indian algorithms?
Studying these algorithms helps us appreciate the rich mathematical heritage of India and challenges misconceptions about the capabilities of ancient civilizations.