This blog explores the fascinating intersection of art, science, and ancient Indian mathematics, particularly focusing on the age-old problem of squaring the circle. We delve into how this challenge was approached and solved in India long before it became a prominent topic in the Western world, highlighting significant contributions from figures like Da Vinci and the teachings of the Sulba Sutras.
Table of Contents
- Intro
- Squaring a Circle is Impossible…
- Threthagni – The 3 Fire Altars
- Squaring a Circle with Sulba Sutras
- Circling a Square with Sulba Sutras
- Sulba Sutrani – Vitruvian Man
- Bhuja Koti Karani Nyayam aka Pythagorean Theorem
- FAQ
Intro
The exploration of geometry is not just a mathematical endeavor; it is an intricate journey that unravels the connections between art, science, and culture. In this section, we delve into the contributions of iconic figures like Leonardo da Vinci and ancient Indian mathematicians, showcasing how their work has shaped our understanding of geometry. The stories behind their masterpieces reveal the harmony between human creativity and mathematical precision.
Scythed Chariot by Da Vinci
Leonardo da Vinci’s fascination with mechanics and engineering is exemplified in his design of the scythed chariot, a remarkable war machine that predates modern engineering concepts. This chariot is not merely a piece of art; it represents a significant leap in the understanding of kinetic energy and mechanical advantage.

Da Vinci meticulously crafted the blueprint for this machine, illustrating how to convert the rotary motion of wheels into a complex gear system. His design foresaw the potential for combining multiple mechanical elements, showcasing a forward-thinking approach that was centuries ahead of its time. The scythed chariot serves as a testament to Da Vinci’s genius, blending artistry with engineering—a theme that resonates throughout his body of work.
The Vitruvian Man
One of Da Vinci’s most famous sketches, the Vitruvian Man, is a profound representation of the proportions of the human body. This iconic image not only captures the anatomical precision of a human figure but also reflects the underlying mathematical principles governing human proportions.

The Vitruvian Man illustrates the concept that the human form is a microcosm of the universe, embodying the principles of symmetry and proportion. Da Vinci’s work in this sketch emphasizes the idea that art and science are intertwined, an understanding that has been a cornerstone of artistic practice since the Renaissance.
The 3 Classic Geometric Problems
Da Vinci’s work is deeply linked to one of the most enduring challenges in mathematics: the three classic geometric problems. These problems—squaring the circle, doubling the cube, and trisecting an angle—have perplexed mathematicians for centuries and highlight the limitations of classical geometry.

- Squaring the Circle: This problem involves constructing a square with the same area as a given circle using only a compass and a straightedge. It has been proven impossible due to the transcendental nature of pi.
- Doubling the Cube: Also known as the Delian problem, it seeks to construct a cube with double the volume of a given cube, which is not achievable with the classical tools.
- Trisecting an Angle: The challenge of dividing an arbitrary angle into three equal parts using only a compass and straightedge has been shown to be impossible for most angles.
The enduring nature of these problems reflects the limits of classical geometry and the quest for solutions that have captivated mathematicians throughout history. Da Vinci’s engagement with these challenges not only showcases his mathematical prowess but also his understanding of the philosophical implications of geometry in the broader context of human inquiry.
Squaring a Circle is Impossible…
The problem of squaring a circle, which has intrigued mathematicians for centuries, is fundamentally rooted in the properties of pi. Pi is a transcendental number, meaning it cannot be expressed as the root of any non-zero polynomial equation with rational coefficients. Consequently, this makes it impossible to construct a square with the same area as a circle using only a compass and straightedge in a finite number of steps. This impossibility was proven in the late 19th century by Ferdinand von Lindemann, who established that squaring the circle is an unattainable goal within the constraints of classical geometry.
Mathematicians from ancient Greeks to Renaissance figures like Da Vinci grappled with this challenge, yet none could find a solution that adhered to the strict guidelines of using only geometric tools. The realization of this impossibility does not diminish the beauty of the problem itself; rather, it highlights the limitations of the tools and methods available to those who sought to solve it.
Threthagni – The 3 Fire Altars
The Tretagni, or the three fire altars, play a crucial role in the ritualistic practices of ancient Indian culture. Each altar serves a distinct purpose and embodies specific geometric principles. The three altars are:
- Grihapatya Yajna: The circular altar, representing the cosmic order and the cyclical nature of existence.
- Dakshinagni Yajna: The semicircular altar, symbolizing the balance between the material and spiritual realms.
- Ahavaniya Yajna: The square altar, embodying stability and the earthly plane.
All three altars must have the same area, a requirement that is not only a mathematical challenge but also carries deep spiritual significance. This requirement ensures that the offerings made during the rituals are balanced, reflecting the harmony sought in the practice of Yajna. The geometric principles governing these constructions are meticulously documented in the Sulba Sutras.

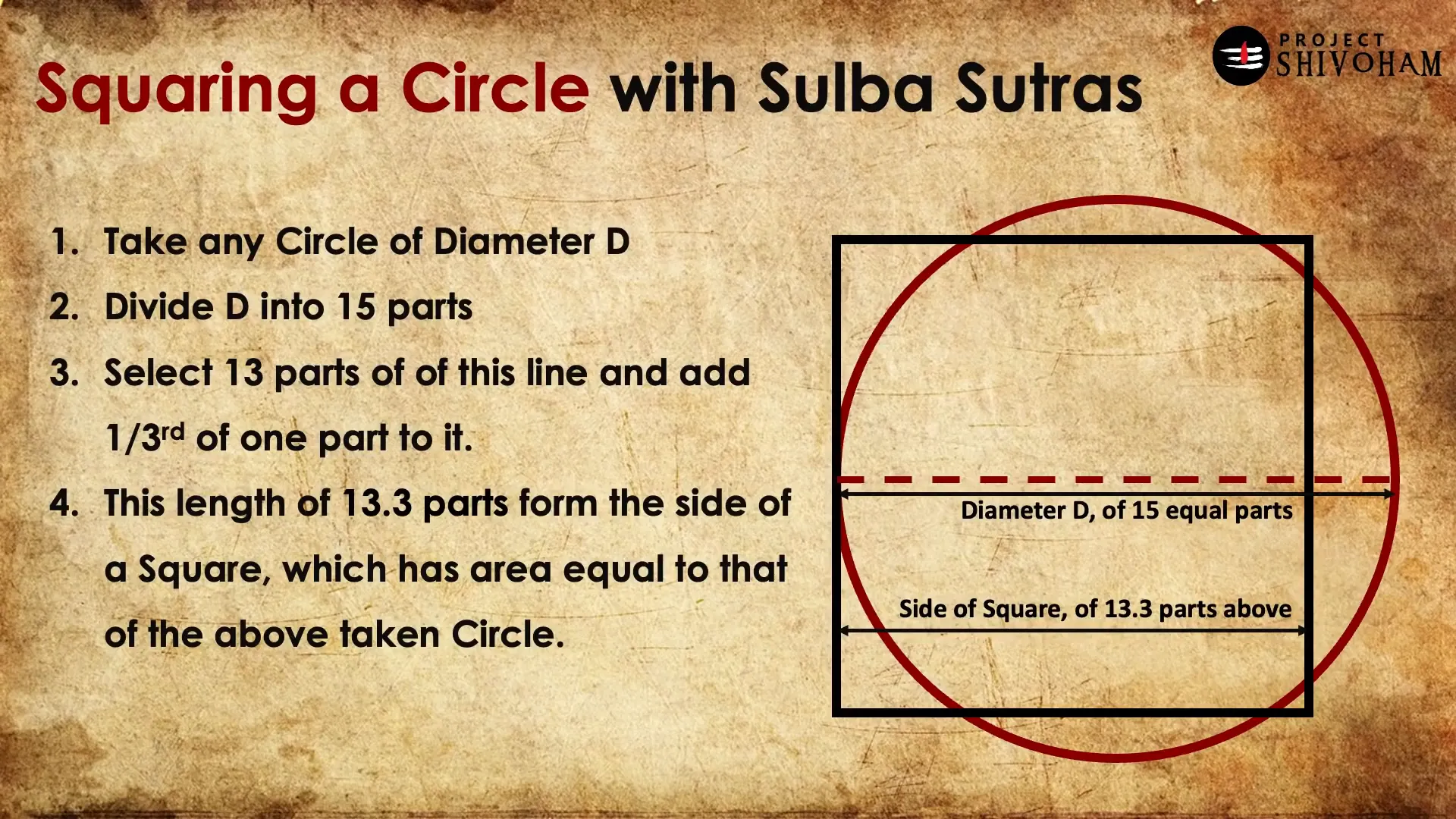
Squaring a Circle with Sulba Sutras
In ancient India, the problem of squaring a circle was approached with remarkable ingenuity. The Sulba Sutras, texts that date back to approximately 800 BCE, provide methods for constructing geometric figures, including the solution to squaring a circle. The formula outlined in these texts offers a practical way to achieve a square with an area equivalent to that of a given circle.
For instance, to square a circle with a diameter of ‘d’, the Sulba Sutras suggest dividing ‘d’ into fifteen equal parts, selecting thirteen parts, and then adding one-third of one part to form the side of the square. This method yields a square whose area is nearly equal to that of the circle, showcasing the advanced understanding of geometry possessed by ancient Indian mathematicians.
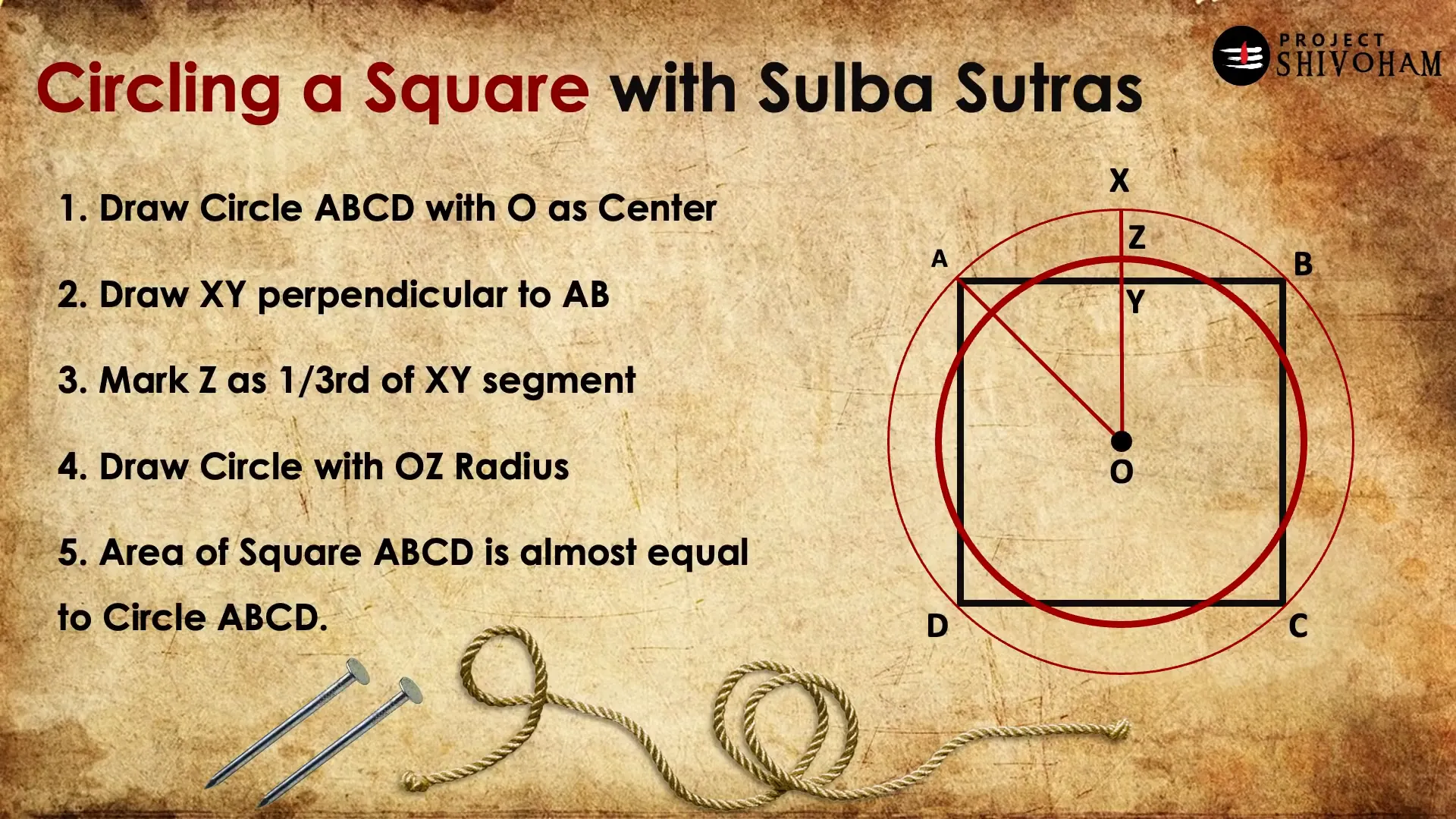
Circling a Square with Sulba Sutras
Similarly, the Sulba Sutras also provide a method for circling a square, where the goal is to construct a circle with an area equal to that of a square. This process involves a straightforward application of geometric principles, allowing practitioners to derive a circle that meets the required area specifications.
Such methods reflect the practical applications of geometry in ancient rituals, demonstrating that the ancient Indian mathematicians were not only solving theoretical problems but also applying their knowledge to real-world situations. The simplicity and elegance of these solutions contrast sharply with the complexity and frustration experienced by those who attempted to solve the same problems using classical Western methods.
The contributions of the Sulba Sutras to geometry are profound, revealing a sophisticated understanding of mathematical principles that were utilized in everyday life and spiritual practices. The legacy of these ancient texts continues to inspire and inform contemporary discussions about the intersection of mathematics, culture, and spirituality.
Sulba Sutrani – Vitruvian Man
The connection between the Sulba Sutras and the Vitruvian Man is profound, as both illustrate the intricate relationship between geometry and the human form. The Vitruvian Man, drawn by Leonardo da Vinci, embodies the idea that the human body is a model of symmetry and proportion, reflecting the principles of geometry that were explored in ancient Indian texts.
In the Sulba Sutras, the emphasis on constructing geometric shapes for various rituals reveals a deep understanding of these principles, much like Da Vinci’s exploration of the human body. The Vitruvian Man’s proportions serve as a visual representation of geometric ideals, paralleling the ancient Indian quest for harmony and balance in design.

Both the Vitruvian Man and the Sulba Sutras highlight the significance of geometry in understanding the world and the human experience. The ancient Indian mathematicians recognized that geometry was not merely a mathematical pursuit; it was a way to connect with the cosmos and the divine. This philosophical underpinning resonates with Da Vinci’s work, where art and science converge.
Bhuja Koti Karani Nyayam aka Pythagorean Theorem
One of the most notable contributions from ancient Indian mathematics is the Bhuja Koti Karani Nyayam, commonly recognized as the Pythagorean theorem. This theorem, attributed to Mahasree Boudhayana, predates Pythagoras and demonstrates a sophisticated understanding of geometric relationships.
The theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This principle has been foundational in both ancient and modern mathematics, revealing how the ancient Indian mathematicians had a grasp of concepts that are still relevant today.

In practice, this theorem was applied in various construction techniques, particularly in the creation of triangular bricks used in traditional architecture. The use of this theorem in real-world applications underscores the practicality of ancient Indian mathematics, which seamlessly integrated theory with practice.
While Pythagoras is often credited with this theorem, it is essential to acknowledge the contributions of Indian scholars who laid the groundwork for these mathematical principles long before he was born. The Bhuja Koti Karani Nyayam stands as a testament to the rich mathematical heritage of Bharat.
FAQ
What are the Sulba Sutras?
The Sulba Sutras are ancient Indian texts that provide instructions on constructing geometric shapes used in Vedic rituals. They contain theorems and formulas that demonstrate an advanced understanding of geometry, predating many Western mathematical concepts.
How does the Vitruvian Man relate to ancient geometry?
The Vitruvian Man illustrates the proportions of the human body based on geometric principles. It embodies the idea that art and science are interconnected, a concept that resonates with the geometric explorations found in the Sulba Sutras.
What is the significance of the Bhuja Koti Karani Nyayam?
The Bhuja Koti Karani Nyayam, or the Pythagorean theorem, is significant because it demonstrates the ancient Indian understanding of geometric relationships in right triangles. Its principles are still used in mathematics and construction today, highlighting the enduring legacy of Indian mathematics.
How were geometric principles applied in ancient Indian rituals?
Geometric principles were essential in constructing fire altars and other shapes used in Vedic rituals. The Sulba Sutras provided guidelines for these constructions, ensuring that they adhered to specific mathematical criteria, which had both practical and spiritual significance.